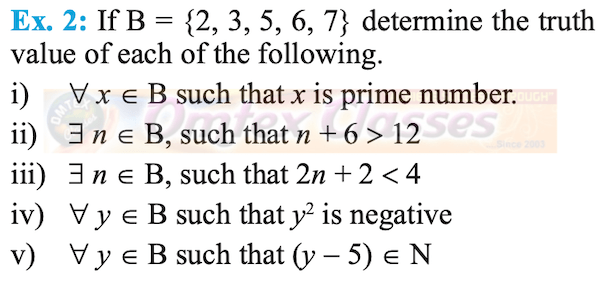Chapter 1: Mathematical Logic
Exercise 1.1
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board
EXERCISE 1.1Q 1 PAGE 2
Exercise 1.1 | Q 1 | Page 2
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
A triangle has ‘n’ sides
SOLUTION
It is an open sentence. Hence, it is not a statement.
[Note: Answer given in the textbook is ‘it is a statement’. However, we found that ‘It is not a statement’.]
EXERCISE 1.1Q 2 PAGE 2
Exercise 1.1 | Q 2 | Page 2
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
The sum of interior angles of a triangle is 180°
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 3 PAGE 2
Exercise 1.1 | Q 3 | Page 2
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
You are amazing!
SOLUTION
It is an exclamatory sentence. Hence, it is not a statement.
EXERCISE 1.1Q 4 PAGE 2
Exercise 1.1 | Q 4 | Page 2
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
Please grant me a loan.
SOLUTION
It is a request. Hence, it is not a statement.
EXERCISE 1.1Q 5 PAGE 2
Exercise 1.1 | Q 5 | Page 2
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
√-4 is an irrational number.
SOLUTION
It is a statement which is false. Hence, it’s truth value is F.
EXERCISE 1.1Q 6 PAGE 2
Exercise 1.1 | Q 6 | Page 2
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
x2 − 6x + 8 = 0 implies x = −4 or x = −2.
SOLUTION
It is a statement which is false. Hence, it’s truth value if F.
EXERCISE 1.1Q 7 PAGE 3
Exercise 1.1 | Q 7 | Page 3
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
He is an actor.
SOLUTION
It is an open sentence. Hence, it is not a statement.
EXERCISE 1.1Q 8 PAGE 3
Exercise 1.1 | Q 8 | Page 3
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
Did you eat lunch yet?
SOLUTION
It is an interrogative sentence. Hence, it is not a statement.
EXERCISE 1.1Q 9 PAGE 3
Exercise 1.1 | Q 9 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
Have a cup of cappuccino.
SOLUTION
It is an imperative sentence, hence it is not a statement.
EXERCISE 1.1Q 10 PAGE 3
Exercise 1.1 | Q 10 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
(x + y)2 = x2 + 2xy + y2 for all x, y ∈ R.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 11 PAGE 3
Exercise 1.1 | Q 11 | Page 3
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
Every real number is a complex number.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 12 PAGE 3
Exercise 1.1 | Q 12 | Page 3
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
1 is a prime number.
SOLUTION
It is a statement which is false. Hence, it’s truth value is F.
EXERCISE 1.1Q 13 PAGE 3
Exercise 1.1 | Q 13 | Page 3
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
With the sunset the day ends.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 14 PAGE 3
Exercise 1.1 | Q 14 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
1 ! = 0
SOLUTION
It is a statement which is false. Hence, it’s truth value is F.
[Note: Answer in the textbook is incorrect]
EXERCISE 1.1Q 15 PAGE 3
Exercise 1.1 | Q 15 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
3 + 5 > 11
SOLUTION
It is a statement which is false. Hence, it’s truth value is F.
EXERCISE 1.1Q 16 PAGE 3
Exercise 1.1 | Q 16 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
The number π is an irrational number.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
[Note: Answer in the textbook is incorrect]
EXERCISE 1.1Q 17 PAGE 3
Exercise 1.1 | Q 17 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
x2 - y2 = (x + y)(x - y) for all x, y ∈ R.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 18 PAGE 3
Exercise 1.1 | Q 18 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
The number 2 is the only even prime number.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 19 PAGE 3
Exercise 1.1 | Q 19 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
Two co-planar lines are either parallel or intersecting.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 20 PAGE 3
Exercise 1.1 | Q 20 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
The number of arrangements of 7 girls in a row for a photograph is 7!.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 21 PAGE 3
Exercise 1.1 | Q 21 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
Give me a compass box.
SOLUTION
It is an imperative sentence. Hence, it is not a statement.
EXERCISE 1.1Q 22 PAGE 3
Exercise 1.1 | Q 22 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
Bring the motor car here.
SOLUTION
It is an imperative sentence. Hence, it is not a statement.
EXERCISE 1.1Q 23 PAGE 3
Exercise 1.1 | Q 23 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
It may rain today.
SOLUTION
It is an open sentence. Hence, it is not a statement.
EXERCISE 1.1Q 24 PAGE 3
Exercise 1.1 | Q 24 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
If a + b < 7, where a ≥ 0 and b ≥ 0 then a < 7 and b < 7.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 25 PAGE 3
Exercise 1.1 | Q 25 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
Can you speak in English?
SOLUTION
It is an interrogative sentence. Hence, it is not a statement.
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.2 [Page 6]
EXERCISE 1.2Q 1.1 PAGE 6
Express the following statement in symbolic form.
e is a vowel or 2 + 3 = 5
SOLUTION
Let p : e is a vowel.
q : 2 + 3 = 5
The symbolic form is p ∨ q.
EXERCISE 1.2Q 1.2 PAGE 6
Express the following statement in symbolic form.
Mango is a fruit but potato is a vegetable.
SOLUTION
Let p : Mango is a fruit.
q : Potato is a vegetable.
The symbolic form is p Λ q.
EXERCISE 1.2Q 1.3 PAGE 6
Express the following statement in symbolic form.
Milk is white or grass is green.
SOLUTION
Let p : Milk is white.
q : Grass is green.
The symbolic form is p ∨ q.
EXERCISE 1.2Q 1.4 PAGE 6
Express the following statement in symbolic form.
I like playing but not singing.
SOLUTION
Let p : I like playing.
q : I do not like singing.
The symbolic form is p ∧ q.
EXERCISE 1.2Q 1.5 PAGE 6
Express the following statement in symbolic form.
Even though it is cloudy, it is still raining.
SOLUTION
Let p : It is cloudy.
q : It is still raining.
The symbolic form is p ∧ q.
EXERCISE 1.2Q 2.1 PAGE 6
Write the truth value of the following statement.
Earth is a planet and Moon is a star.
SOLUTION
Let p : Earth is a planet.
q : Moon is a star.
The truth values of p and q are T and F respectively.
The given statement in symbolic form is p ∧ q.
∴ p ∧ q ≡ T ∧ F ≡ F
∴ Truth value of the given statement is F.
EXERCISE 1.2Q 2.2 PAGE 6
Write the truth value of the following statement.
16 is an even number and 8 is a perfect square.
SOLUTION
Let p : 16 is an even number.
q : 8 is a perfect square.
The truth values of p and q are T and F respectively.
The given statement in symbolic form is p ∧ q.
∴ p ∧ q ≡ T ∧ F ≡ F
∴ Truth value of the given statement is F.
EXERCISE 1.2Q 2.3 PAGE 6
Write the truth value of the following statement.
A quadratic equation has two distinct roots or 6 has three prime factors.
SOLUTION
Let p : A quadratic equation has two distinct roots.
q : 6 has three prime factors.
The truth values of p and q are F and F respectively.
The given statement in symbolic form is p ∨ q.
∴ p ∨ q ≡ F ∨ F ≡ F
∴ Truth value of the given statement is F.
EXERCISE 1.2Q 2.4 PAGE 6
Write the truth value of the following statement.
The Himalayas are the highest mountains but they are part of India in the North East.
SOLUTION
Let p : Himalayas are the highest mountains.
q : Himalayas are the part of India in the north east.
The truth values of p and q are T and T respectively.
The given statement in symbolic form is p ∧ q.
∴ p ∧ q ≡ T ∧ T ≡ T
∴ Truth value of the given statement is T.
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.3 [Page 7]
EXERCISE 1.3Q 1.1 PAGE 7
Write the negation of the following statement.
All men are animals.
SOLUTION
Some men are not animals.
EXERCISE 1.3Q 1.2 PAGE 7
Write the negation of the following statement.
− 3 is a natural number.
SOLUTION
– 3 is not a natural number.
EXERCISE 1.3Q 1.3 PAGE 7
Write the negation of the following statement.
It is false that Nagpur is capital of Maharashtra
SOLUTION
Nagpur is capital of Maharashtra.
EXERCISE 1.3Q 1.4 PAGE 7
Write the negation of the following statement.
2 + 3 ≠ 5
SOLUTION
2 + 3 = 5
EXERCISE 1.3Q 2.1 PAGE 7
Write the truth value of the negation of the following statement.
√5 is an irrational number.
SOLUTION
Truth value of the given statement is T.
∴ Truth value of its negation is F.
EXERCISE 1.3Q 2.2 PAGE 7
Write the truth value of the negation of the following statement.
London is in England.
SOLUTION
Truth value of the given statement is T.
∴ Truth value of its negation is F.
EXERCISE 1.3Q 2.3 PAGE 7
Write the truth value of the negation of the following statement.
For every x ∈ N, x + 3 < 8.
SOLUTION
Truth value of the given statement is F.
∴ Truth value of its negation is T.
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.4 [Pages 10 - 11]
Write the following statement in symbolic form.
If triangle is equilateral then it is equiangular.
SOLUTION
Let p : Triangle is equilateral.
q : Triangle is equiangular.
The symbolic form is p → q.
Write the following statement in symbolic form.
It is not true that “i” is a real number.
SOLUTION
Let p : i is a real number.
The symbolic form is ~ p.
Write the following statement in symbolic form.
Even though it is not cloudy, it is still raining.
SOLUTION
Let p : It is cloudy.
q : It is raining.
The symbolic form is ~p ∧ q.
Write the following statement in symbolic form.
Milk is white if and only if the sky is not blue.
SOLUTION
Let p : Milk is white.
q : Sky is blue.
The symbolic form is p ↔ ~ q.
Write the following statement in symbolic form.
Stock prices are high if and only if stocks are rising.
SOLUTION
Let p : Stock prices are high.
q : Stock are rising
The symbolic form is p ↔ q.
Write the following statement in symbolic form.
If Kutub-Minar is in Delhi then Taj-Mahal is in Agra.
SOLUTION
Let p : Kutub-Minar is in Delhi.
q : Taj-Mahal Is in Agra.
The symbolic form is p → q.
Find the truth value of the following statement.
It is not true that 3 − 7i is a real number.
SOLUTION
Let p : 3 – 7i is a real number.
The truth value of p is F.
The given statement in symbolic form is ~p.
∴ ~ p ≡ ~ F ≡ T
∴ Truth value of the given statement is T.
Find the truth value of the following statement.
If a joint venture is a temporary partnership, then discount on purchase is credited to the supplier.
SOLUTION
Let p : A joint venture is a temporary partnership. q : Discount on purchase is credited to the supplier.
The truth value of p and q are T and F respectively.
The given statement in symbolic form is p → q.
∴ p → q ≡ T → F ≡ F
∴ Truth value of the given statement is F.
Find the truth value of the following statement.
Every accountant is free to apply his own accounting rules if and only if machinery is an asset.
SOLUTION
Let p : Every accountant is free to apply his own accounting rules.
q : Machinery is an asset.
The truth values of p and q are F and T respectively.
The given statement in symbolic form is p ↔ q.
∴ p ↔ q ≡ F ↔ T ≡ F
∴ Truth value of the given statement is F.
Find the truth value of the following statement.
Neither 27 is a prime number nor divisible by 4.
SOLUTION
Let p : 27 is a prime number.
q : 27 is divisible by 4.
The truth values of p and q are F and F respectively.
The given statement in symbolic form is ~ p ∧ ~ q.
∴ ~ p ∧ ~ q ≡ ~ F ∧ ~ F ≡ T ∧ T ≡ T
∴ Truth value of the given statement is T.
Find the truth value of the following statement.
3 is a prime number and an odd number.
SOLUTION
Let p : 3 is a prime number.
q : 3 is an odd number.
The truth values of p and q are T and T respectively.
The given statement in symbolic form is p ∧ q.
∴ p ∧ q ≡ T ∧ T ≡ T
∴ Truth value of the given statement is T.
If p and q are true and r and s are false, find the truth value of the following compound statement.
p ∧ (q ∧ r)
SOLUTION
p ∧ (q ∧ r) ≡ T ∧ (T ∧ F)
≡ T ∧ F
≡ F
Hence, truth value if F.
If p and q are true and r and s are false, find the truth value of the following compound statement.
(p → q) ∨ (r ∧ s)
SOLUTION
(p → q) ∨ (r ∧ s) ≡ (T → T) ∨ (F ∧ F)
≡ T ∨ F
≡ T
Hence, truth value if T.
If p and q are true and r and s are false, find the truth value of the following compound statement.
~ [(~ p ∨ s) ∧ (~ q ∧ r)]
SOLUTION
~ [(~ p ∨ s) ∧ (~ q ∧ r)] ≡ ~[(~T ∨ F) ∧ (~T ∧ F)]
≡ ~[(F ∨ F) ∧ (F ∧ F)
≡ ~ (F ∧ F)
≡ ~ F
≡ T
Hence, truth value if T.
If p and q are true and r and s are false, find the truth value of the following compound statement.
(p → q) ↔ ~(p ∨ q)
SOLUTION
(p → q) ↔ ~(p ∨ q) ≡ (T → T) ↔ (T ∨ T)
≡ T ↔ ~ T
≡ T ↔ F
≡ F
Hence, truth value if F.
If p and q are true and r and s are false, find the truth value of the following compound statement.
[(p ∨ s) → r] ∨ ~ [~ (p → q) ∨ s]
SOLUTION
[(p ∨ s) → r] ∨ ~ [~ (p → q) ∨ s]
≡ [(T ∨ F) → F] ∨ ~[~ (T → T) ∨ F]
≡ (T → F) ∨ ~ (~ T ∨ F)
≡ F ∨ ~ (F ∨ F)
≡ F ∨ ~ F
≡ F ∨ T
≡ T
Hence, truth value is T.
If p and q are true and r and s are false, find the truth value of the following compound statement.
~ [p ∨ (r ∧ s)] ∧ ~ [(r ∧ ~ s) ∧ q]
SOLUTION
~ [p ∨ (r ∧ s)] ∧ ~ [(r ∧ ~ s) ∧ q]
≡ ~ [T ∨ (F ∧ F)] ∧ ~ [(F ∧ ~ F) ∧ T]
≡ ~ (T ∨ F) ∧ ~ [(F ∧ T) ∧ T]
≡ ~ T ∧ ~ (F ∧ T)
≡ F ∧ ~ F
≡ F ∧ T
≡ F
Hence, truth value is F.
Assuming that the following statement is true,
p : Sunday is holiday,
q : Ram does not study on holiday,
find the truth values of the following statements.
Sunday is not holiday or Ram studies on holiday.
SOLUTION
Symbolic form of the given statement is ~ p ∨~q
∴ ~ p ∨~ q ≡ ~ T ∨ ~ T
≡ F ∨ F
≡ F
Hence, truth value is F.
Assuming that the following statement is true,
p : Sunday is holiday,
q : Ram does not study on holiday,
find the truth values of the following statements.
If Sunday is not holiday then Ram studies on holiday.
SOLUTION
Symbolic form of the given statement is
~ p → ~ q
∴ ~ p → ~ q ≡ ~ T → ~ T
≡ F → F
≡ T
Hence, truth value is T.
Assuming that the following statement is true,
p : Sunday is holiday,
q : Ram does not study on holiday,
find the truth values of the following statements.
Sunday is a holiday and Ram studies on holiday.
SOLUTION
Symbolic form of the given statement is p ∧ ~ q
∴ p ∧ ~ q ≡ T ∧ ~ T
≡ T ∧ F
≡ F
Hence, truth value is F.
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
p ↔ ~ q
SOLUTION
He swims if and only if water is not warm.
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
~ (p ∨ q)
SOLUTION
It is not true that he swims or water is warm.
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
q → p
SOLUTION
If water is warm then he swims.
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
q ∧ ~ p
SOLUTION
Water is warm and he does not swim.
EXERCISE 1.5PAGE 12
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.5 [Page 12]
Use quantifiers to convert the following open sentences defined on N, into a true statement.
x2 + 3x - 10 = 0
SOLUTION
∃ x ∈ N, such that x2 + 3x – 10 = 0
It is true statement, since x = 2 ∈ N satisfies it.
Use quantifiers to convert the following open sentences defined on N, into a true statement.
3x - 4 < 9
SOLUTION
∃ x ∈ N, such that 3x – 4 < 9
It is true statement, since
x = 2, 3, 4 ∈ N satisfies 3x - 4 < 9.
Use quantifiers to convert the following open sentences defined on N, into a true statement.
n2 ≥ 1
SOLUTION
∀ n ∈ N, n2 ≥ 1
It is true statement, since all n ∈ N satisfy it.
Use quantifiers to convert the following open sentences defined on N, into a true statement.
2n - 1 = 5
SOLUTION
∃ n ∈ N, such that 2n - 1 = 5
It is a true statement since all n = 3 ∈ N satisfy 2n - 1 = 5.
Use quantifiers to convert the following open sentences defined on N, into a true statement.
y + 4 > 6
SOLUTION
∃ y ∈ N, such that y + 4 > 6
It is a true statement since y = 3, 4, ... ∈ N satisfy y + 4 > 6.
Use quantifiers to convert the following open sentences defined on N, into a true statement.
3y - 2 ≤ 9
SOLUTION
∃ y ∈ N, such that 3y - 2 ≤ 9
It is a true statement since y = 1, 2, 3 ∈ N satisfy it.
If B = {2, 3, 5, 6, 7} determine the truth value of ∀ x ∈ B such that x is prime number.
SOLUTION
For x = 6, x is not a prime number.
∴ x = 6 does not satisfies the given statement.
∴ The given statement is false.
∴ It’s truth value is F.
If B = {2, 3, 5, 6, 7} determine the truth value of
∃ n ∈ B, such that n + 6 > 12.
SOLUTION
For n = 7, n + 6 = 7 + 6 = 13 > 12
∴ n = 7 satisfies the equation n + 6 > 12.
∴ The given statement is true.
∴ It’s truth value is T.
If B = {2, 3, 5, 6, 7} determine the truth value of
∃ n ∈ B, such that 2n + 2 < 4.
SOLUTION
There is no n in B which satisfies 2n + 2 < 4.
∴ The given statement is false.
∴ It’s truth value is F.
If B = {2, 3, 5, 6, 7} determine the truth value of
∀ y ∈ B, such that y2 is negative.
SOLUTION
There is no y in B which satisfies y2 < 0.
∴ The given statement is false.
∴ It’s truth value is F.
If B = {2, 3, 5, 6, 7} determine the truth value of
∀ y ∈ B, such that (y - 5) ∈ N
SOLUTION
For y = 2, y – 5 = 2 – 5 = –3 ∉ N.
∴ y = 2 does not satisfies the equation (y – 5) ∈ N.
∴ The given statement is false.
∴ It’s truth value is F.
EXERCISE 1.6PAGE 16
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.6 [Page 16]
Prepare truth tables for the following statement pattern.
p → (~ p ∨ q)
SOLUTION
p → (~ p ∨ q)
| p | q | ~p | ~ p ∨ q | p → (~ p ∨ q) |
| T | T | F | T | T |
| T | F | F | F | F |
| F | T | T | T | T |
| F | F | T | T | T |
Prepare truth tables for the following statement pattern.
(~ p ∨ q) ∧ (~ p ∨ ~ q)
SOLUTION
(~ p ∨ q) ∧ (~ p ∨ ~ q)
| p | q | ~p | ~q | ~p∨q | ~p∨~q | (~p∨q)∧(~p∨~q) |
| T | T | F | F | T | F | F |
| T | F | F | T | F | T | F |
| F | T | T | F | T | T | T |
| F | F | T | T | T | T | T |
Prepare truth tables for the following statement pattern.
(p ∧ r) → (p ∨ ~ q)
SOLUTION
(p ∧ r) → (p ∨ ~ q)
| p | q | r | ~q | p ∧ r | p∨~q | (p ∧ r) → (p ∨ ~ q) |
| T | T | T | F | T | T | T |
| T | T | F | F | F | T | T |
| T | F | T | T | T | T | T |
| T | F | F | T | F | T | T |
| F | T | T | F | F | F | T |
| F | T | F | F | F | F | T |
| F | F | T | T | F | T | T |
| F | F | F | T | F | T | T |
Prepare truth tables for the following statement pattern.
(p ∧ q) ∨ ~ r
SOLUTION
(p ∧ q) ∨ ~ r
| p | q | r | ~r | p ∧ q | (p ∧ q) ∨ ~ r |
| T | T | T | F | T | T |
| T | T | F | T | T | T |
| T | F | T | F | F | F |
| T | F | F | T | F | T |
| F | T | T | F | F | F |
| F | T | F | T | F | T |
| F | F | T | F | F | F |
| F | F | F | T | F | T |
Examine whether the following statement pattern is a tautology, a contradiction or a contingency.
q ∨ [~ (p ∧ q)]
SOLUTION
| p | q | p ∧ q | ~ (p ∧ q) | q ∨ [~ (p ∧ q)] |
| T | T | T | F | T |
| T | F | F | T | T |
| F | T | F | T | T |
| F | F | F | T | T |
All the truth values in the last column are T. Hence, it is a tautology.
Examine whether the following statement pattern is a tautology, a contradiction or a contingency.
(~ q ∧ p) ∧ (p ∧ ~ p)
SOLUTION
| p | q | ~p | ~q | (~q∧p) | (p∧~p) | (~q∧p)∧(p∧~p) |
| T | T | F | F | F | F | F |
| T | F | F | T | T | F | F |
| F | T | T | F | F | F | F |
| F | F | T | T | F | F | F |
All the truth values in the last column are F. Hence, it is a contradiction.
Examine whether the following statement pattern is a tautology, a contradiction or a contingency.
(p ∧ ~ q) → (~ p ∧ ~ q)
SOLUTION
| p | q | ~p | ~q | p∧~q | ~p∧~q | (p∧~q)→(~p∧~q) |
| T | T | F | F | F | F | T |
| T | F | F | T | T | F | F |
| F | T | T | F | F | F | T |
| F | F | T | T | F | T | T |
The truth values in the last column are not identical. Hence, it is contingency.
Examine whether the following statement pattern is a tautology, a contradiction or a contingency.
~ p → (p → ~ q)
SOLUTION
| p | q | ~p | ~q | p→~q | ~p→(p→~q) |
| T | T | F | F | F | T |
| T | F | F | T | T | T |
| F | T | T | F | T | T |
| F | F | T | T | T | T |
All the truth values in the last column are T. Hence, it is tautology.
Prove that the following statement pattern is a tautology.
(p ∧ q) → q
SOLUTION
| p | q | p ∧ q | (p∧q)→q |
| T | T | T | T |
| T | F | F | T |
| F | T | F | T |
| F | F | F | T |
All the truth values in the last column are T. Hence, it is tautology.
Prove that the following statement pattern is a tautology.
(p → q) ↔ (~ q → ~ p)
SOLUTION
| p | q | ~p | ~q | p→q | ~q→~p | (p→q)↔(~q→~p) |
| T | T | F | F | T | T | T |
| T | F | F | T | F | F | T |
| F | T | T | F | T | T | T |
| F | F | T | T | T | T | T |
All the truth values in the last column are T. Hence, it is a tautology.
Prove that the following statement pattern is a tautology.
(~p ∧ ~q ) → (p → q)
SOLUTION
| p | q | ~p | ~q | ~p∧~q | p→q | (~p∧~q)→(p→q) |
| T | T | F | F | F | T | T |
| T | F | F | T | F | F | T |
| F | T | T | F | F | T | T |
| F | F | T | T | T | T | T |
All the truth values in the last column are T. Hence, it is a tautology.
Prove that the following statement pattern is a tautology.
(~ p ∨ ~ q) ↔ ~ (p ∧ q)
SOLUTION
| p | q | ~p | ~q | ~p∨~q | p∧q | ~p∨~q | (~p∨~q↔~(p ∧ q) |
| T | T | F | F | F | T | F | T |
| T | F | F | T | T | F | T | T |
| F | T | T | F | T | F | T | T |
| F | F | T | T | T | F | T | T |
All the truth values in the last column are T. Hence, it is a tautology.
Prove that the following statement pattern is a contradiction.
(p ∨ q) ∧ (~p ∧ ~q)
SOLUTION
| p | q | ~p | ~q | p∨q | ~p∧~q | (p∨q)∧(~p∧~q) |
| T | T | F | F | T | F | F |
| T | F | F | T | T | F | F |
| F | T | T | F | T | F | F |
| F | F | T | T | F | T | F |
All the truth values in the last column are F. Hence, it is a contradiction.
Prove that the following statement pattern is a contradiction.
(p ∧ q) ∧ ~p
SOLUTION
| p | q | ~p | p∧q | (p∧q)∧~p |
| T | T | F | T | F |
| T | F | F | F | F |
| F | T | T | F | F |
| F | F | T | F | F |
All the truth values in the last column are F. Hence, it is a contradiction.
Prove that the following statement pattern is a contradiction.
(p ∧ q) ∧ (~p ∨ ~q)
SOLUTION
| p | q | ~p | ~q | p∧q | ~p∨~q | (p∧q)∧(~p∨~q) |
| T | T | F | F | T | F | F |
| T | F | F | T | F | T | F |
| F | T | T | F | F | T | F |
| F | F | T | T | F | T | F |
All the truth values in the last column are F. Hence, it is a contradiction.
Prove that the following statement pattern is a contradiction.
(p → q) ∧ (p ∧ ~ q)
SOLUTION
| p | q | ~q | p→q | p∧~q | (p→q)∧(p∧~q) |
| T | T | F | T | F | F |
| T | F | T | F | T | F |
| F | T | F | T | F | F |
| F | F | T | T | F | F |
All the truth values in the last column are F. Hence, it is a contradiction.
Show that the following statement pattern is contingency.
(p∧~q) → (~p∧~q)
SOLUTION
| p | q | ~p | ~q | p∧~q | ~p∧~q | (p∧~q)→(~p∧~q) |
| T | T | F | F | F | F | T |
| T | F | F | T | T | F | F |
| F | T | T | F | F | F | T |
| F | F | T | T | F | T | T |
The truth values in the last column are not identical. Hence, it is contingency.
Show that the following statement pattern is contingency.
(p → q) ↔ (~ p ∨ q)
SOLUTION
| p | q | ~p | p→q | ~p∨q | (p→q)↔(~p∨q) |
| T | T | F | T | T | T |
| T | F | F | F | F | T |
| F | T | T | T | T | T |
| F | F | T | T | T | T |
All the truth values in the last column are T. Hence, it is a tautology. Not contingency.
Show that the following statement pattern is contingency.
p ∧ [(p → ~ q) → q]
SOLUTION
| p | q | ~q | p→~q | (p→~q)→q | p∧[(p→~q)→q] |
| T | T | F | F | T | T |
| T | F | T | T | F | F |
| F | T | F | T | T | F |
| F | F | T | T | F | F |
Truth values in the last column are not identical. Hence, it is contingency.
Show that the following statement pattern is contingency.
(p → q) ∧ (p → r)
SOLUTION
| p | q | r | p→q | p→r | (p→q)∧(p→r) |
| T | T | T | T | T | T |
| T | T | F | T | F | F |
| T | F | T | F | T | F |
| T | F | F | F | F | F |
| F | T | T | T | T | T |
| F | T | F | T | T | T |
| F | F | T | T | T | T |
| F | F | F | T | T | T |
The truth values in the last column are not identical. Hence, it is contingency.
Exercise 1.6 | Q 6.1 | Page 16
Using the truth table, verify
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| p | q | r | q∧r | p∨(q∧r) | p∨q | p∨r | (p∨q)∧(p∨r) |
| T | T | T | T | T | T | T | T |
| T | T | F | F | T | T | T | T |
| T | F | T | F | T | T | T | T |
| T | F | F | F | T | T | T | T |
| F | T | T | T | T | T | T | T |
| F | T | F | F | F | T | F | F |
| F | F | T | F | F | F | T | F |
| F | F | F | F | F | F | F | F |
The entries in columns 5 and 8 are identical.
∴ p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
Using the truth table, verify
p → (p → q) ≡ ~ q → (p → q)
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 |
| p | q | ~q | p→q | p→(p→q) | ~q→(p→q) |
| T | T | F | T | T | T |
| T | F | T | F | F | F |
| F | T | F | T | T | T |
| F | F | T | T | T | T |
In the above truth table, entries in columns 5 and 6 are identical.
∴ p → (p → q) ≡ ~ q → (p → q)
Using the truth table, verify
~(p → ~q) ≡ p ∧ ~ (~ q) ≡ p ∧ q
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| p | q | ~q | p→~q | ~(p→~q) | ~(~q) | p∧~(~q) | p∧q |
| T | T | F | F | T | T | T | T |
| T | F | T | T | F | F | F | F |
| F | T | F | T | F | T | F | F |
| F | F | T | T | F | F | F | F |
In the above table, entries in columns 5, 7, and 8 are identical.
∴ ~(p → ~q) ≡ p ∧ ~ (~ q) ≡ p ∧ q
Using the truth table, verify
~(p ∨ q) ∨ (~ p ∧ q) ≡ ~ p
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| p | q | ~p | (p∨q) | ~(p∨q) | ~p∧q | ~(p∨q)∨(~p∧q) |
| T | T | F | T | F | F | F |
| T | F | F | T | F | F | F |
| F | T | T | T | F | T | T |
| F | F | T | F | T | F | T |
In the above truth table, the entries in columns 3 and 7 are identical.
∴ ~(p ∨ q) ∨ (~ p ∧ q) ≡ ~ p
Exercise 1.6 | Q 7.1 | Page 16
Using the truth table, verify
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| p | q | r | q∧r | p∨(q∧r) | p∨q | p∨r | (p∨q)∧(p∨r) |
| T | T | T | T | T | T | T | T |
| T | T | F | F | T | T | T | T |
| T | F | T | F | T | T | T | T |
| T | F | F | F | T | T | T | T |
| F | T | T | T | T | T | T | T |
| F | T | F | F | F | T | F | F |
| F | F | T | F | F | F | T | F |
| F | F | F | F | F | F | F | F |
The entries in columns 5 and 8 are identical.
∴ ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
Prove that the following pair of statement pattern is equivalent.
p ↔ q and (p → q) ∧ (q → p)
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 |
| p | q | p↔q | p→q | q→p | (p→q)∧(q→p) |
| T | T | T | T | T | T |
| T | F | F | F | T | F |
| F | T | F | T | F | F |
| F | F | T | T | T | T |
In the above table, entries in columns 3 and 6 are identical.
∴ Statement p ↔ q and (p → q) ∧ (q → p) are equivalent.
Prove that the following pair of statement pattern is equivalent.
p → q and ~ q → ~ p and ~ p ∨ q
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| p | q | ~p | ~q | p→q | ~q→~p | ~p∨q |
| T | T | F | F | T | T | T |
| T | F | F | T | F | F | F |
| F | T | T | F | T | T | T |
| F | F | T | T | T | T | T |
In the above table, entries in columns 5, 6 and 7 are identical.
∴ Statement p → q and ~q → ~p and ~p ∨ q are equivalent.
Prove that the following pair of statement pattern is equivalent.
~(p ∧ q) and ~p ∨ ~q
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| p | q | ~p | ~q | p∧q | ~(p∧q) | ~p∨~q |
| T | T | F | F | T | F | F |
| T | F | F | T | F | T | T |
| F | T | T | F | F | T | T |
| F | F | T | T | F | T | T |
In the above table, entries in columns 6 and 7 are identical.
∴ Statement ~(p ∧ q) and ~p ∨ ~q are equivalent.
EXERCISE 1.7PAGE 17
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.7 [Page 17]
Write the dual of the following:
(p ∨ q) ∨ r
SOLUTION
(p ∧ q) ∧ r
Write the dual of the following:
~(p ∨ q) ∧ [p ∨ ~ (q ∧ ~ r)]
SOLUTION
~(p ∧ q) ∨ [p ∧ ~ (q ∨ ~ r)]
Write the dual of the following:
p ∨ (q ∨ r) ≡ (p ∨ q) ∨ r
SOLUTION
p ∧ (q ∧ r) ≡ (p ∧ q) ∧ r
Write the dual of the following:
~(p ∧ q) ≡ ~ p ∨ ~ q
SOLUTION
~(p ∨ q) ≡ ~ p ∧ ~ q
Write the dual statement of the following compound statement.
13 is a prime number and India is a democratic country.
SOLUTION
13 is a prime number or India is a democratic country.
Write the dual statement of the following compound statement.
Karina is very good or everybody likes her.
SOLUTION
Karina is very good and everybody likes her.
Write the dual statement of the following compound statement.
Radha and Sushmita cannot read Urdu.
SOLUTION
Radha or Sushmita cannot read Urdu.
Write the dual statement of the following compound statement.
A number is a real number and the square of the number is non-negative.
SOLUTION
A number is a real number or the square of the number is non-negative.